A graph generally represents a network of nodes or a hierarchy. In real life, it could be a network of roads, people or computers, or a hierarchy of employees in a company. A social network like LinkedIn or Instagram has users as the nodes; the edges between the nodes represent the connections or links.

We can represent this network or a graph visually in the following ways:

1. Grid

2. Cluster of Nodes

3. Hierarchy

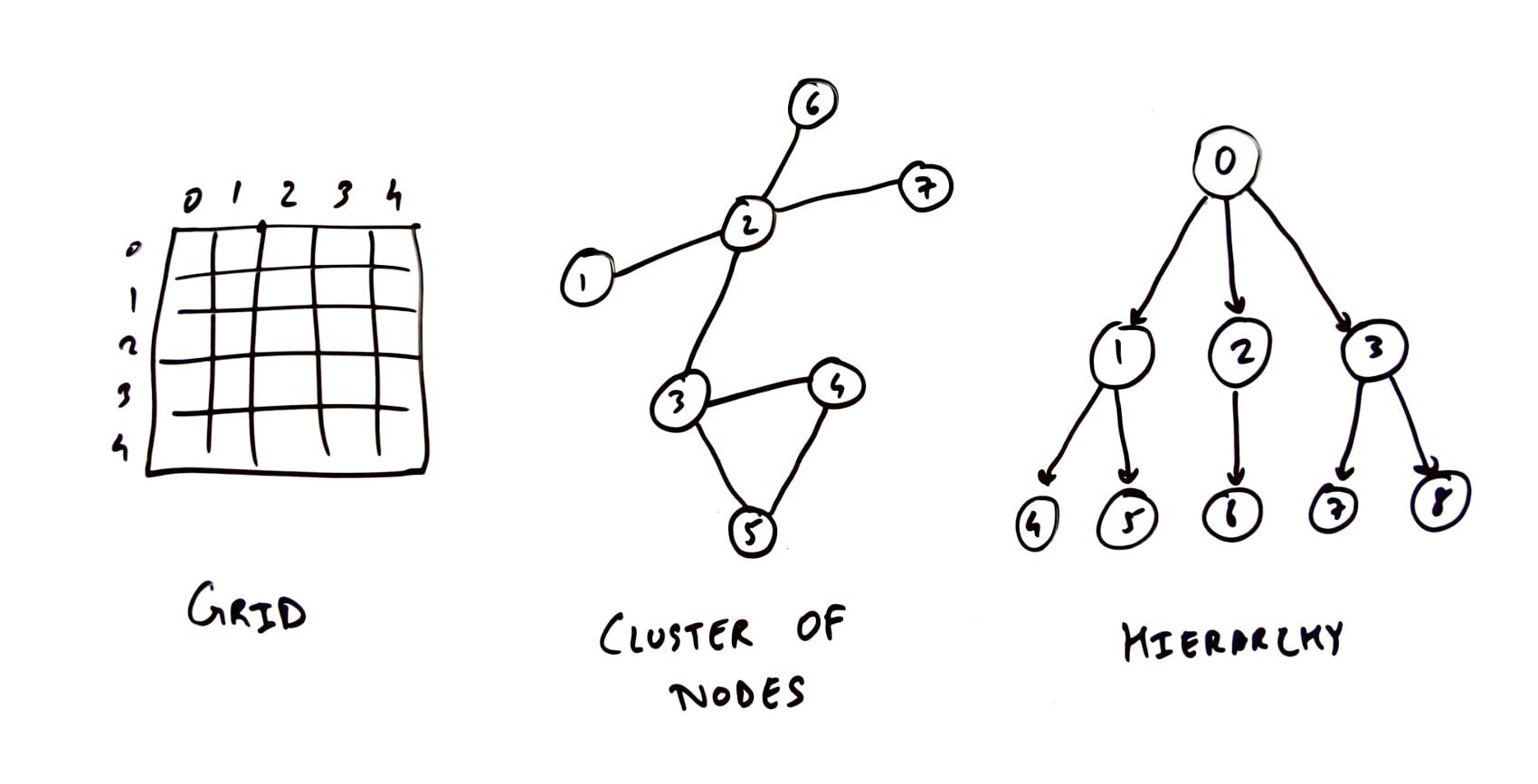
Different Representations of Graphs - TechBum.io

Let's look at the different data structures we can use as building blocks for designing a Graph. If you have read about Graphs before, terms like adjacency matrix and adjacency lists might sound familiar. But in this tutorial, I want to try and simplify the graph data structure fundamentals by adding my spin to it.

1. Grid, Mesh, or Matrix

As you might have guessed, we can use a simple matrix or a multi-dimensional structure to represent a graph. When solving coding interview questions, these commonly come up as an area or space like a room or island.

For flavors of graph problems,

1. In a room or maze of size 5 x 5, we want to make our robot find its way from a given starting point to a target point while avoiding obstacles.

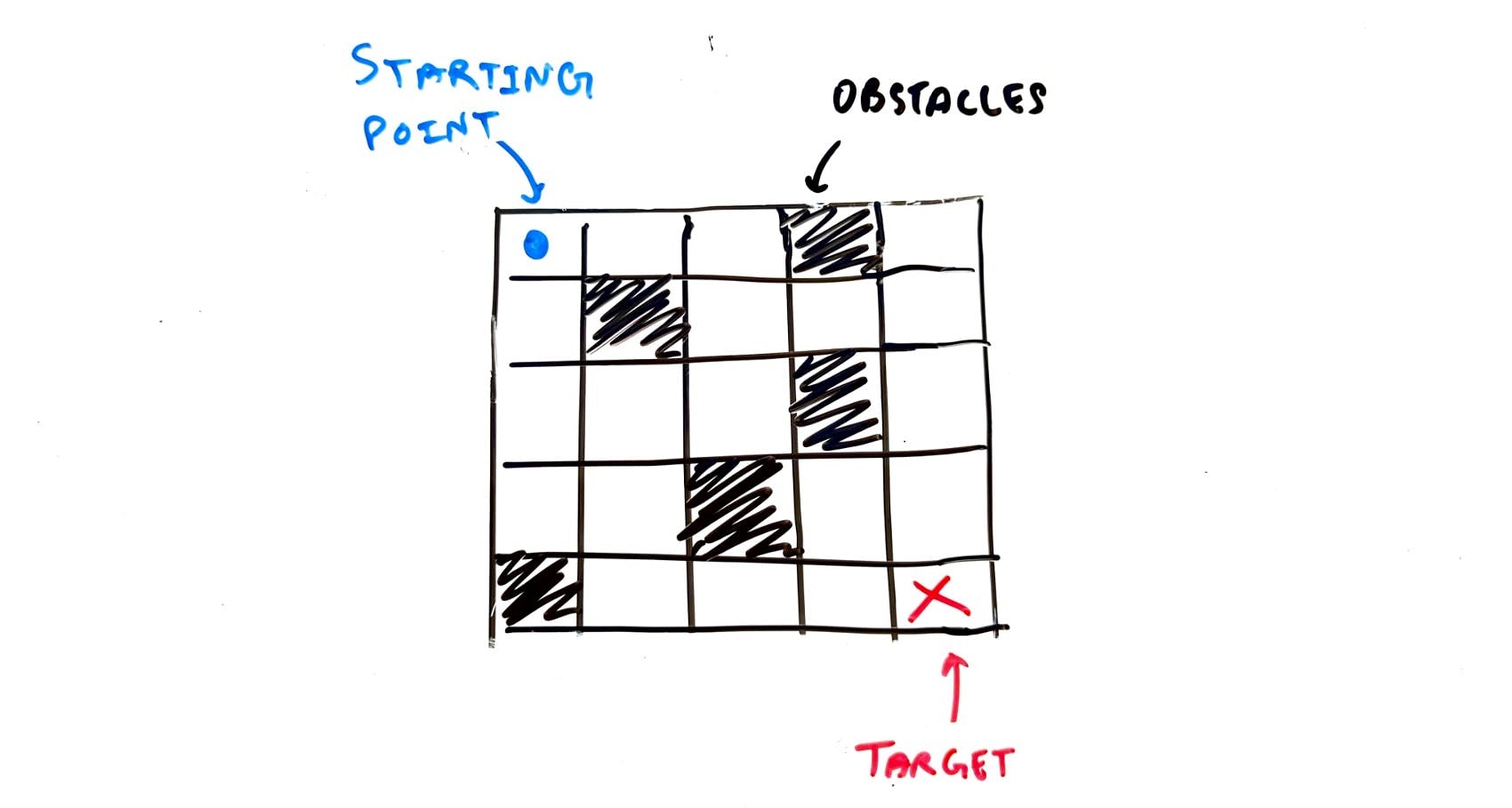
Room or Maze as a Graph Problem - TechBum.io

Few follow-ups could be:
  a. Count the number of unique paths from source to destination.
  b. Determine the shortest path from source to destination.

2. In a 10 x 10 grid, each tile is marked with 0 or 1, 0 for water, and 1 for land. Given that an island is a connected land mass surrounded by water, in this case, a cluster of 1's surrounded by 0's, find the number of islands on the map.

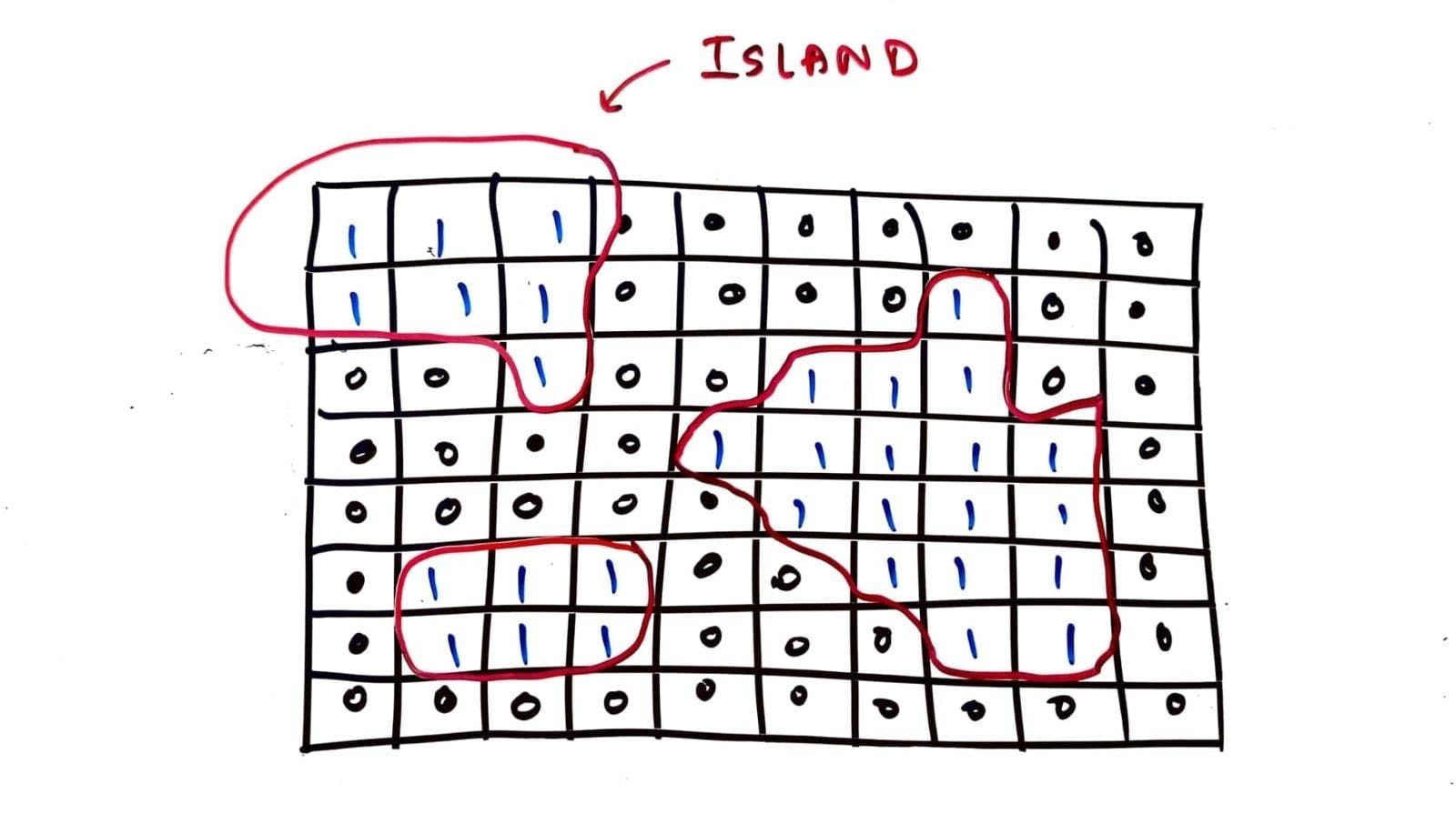
Island type Graph Problems - TechBum.io

A follow-up question could be:
  a. Determine the area of the smallest or biggest island.

Problems like these are good candidates to be represented as a matrix as it has a reasonable memory footprint for maintaining the N x N matrix. In general, Matrix is suitable for representing densely connected nodes. Meaning, that each Node is connected to most other Nodes in the graph, a.k.a, maximally connected.

2. Sparse Network or Low-Density Network

Now let's think about when a matrix would not be a good choice of data structure to represent a Graph. Let's take an example of a Social Network that has 100 users. If we are to build a matrix, we would be representing it as a 100 x 100 matrix. This will allow us to map 10,000 edges that represent the following & follower relationships. But let's say each user is connected to approx 3 other users in the network, which can probably be represented by approx 500 edges. Maintaining a 100 x 100 matrix in memory is extremely wasteful and leads to high space complexity.

To overcome this, we have two options, either build a Linked Node data structure or use a Map, HashMap, or Dictionary to maintain our graph data structure.

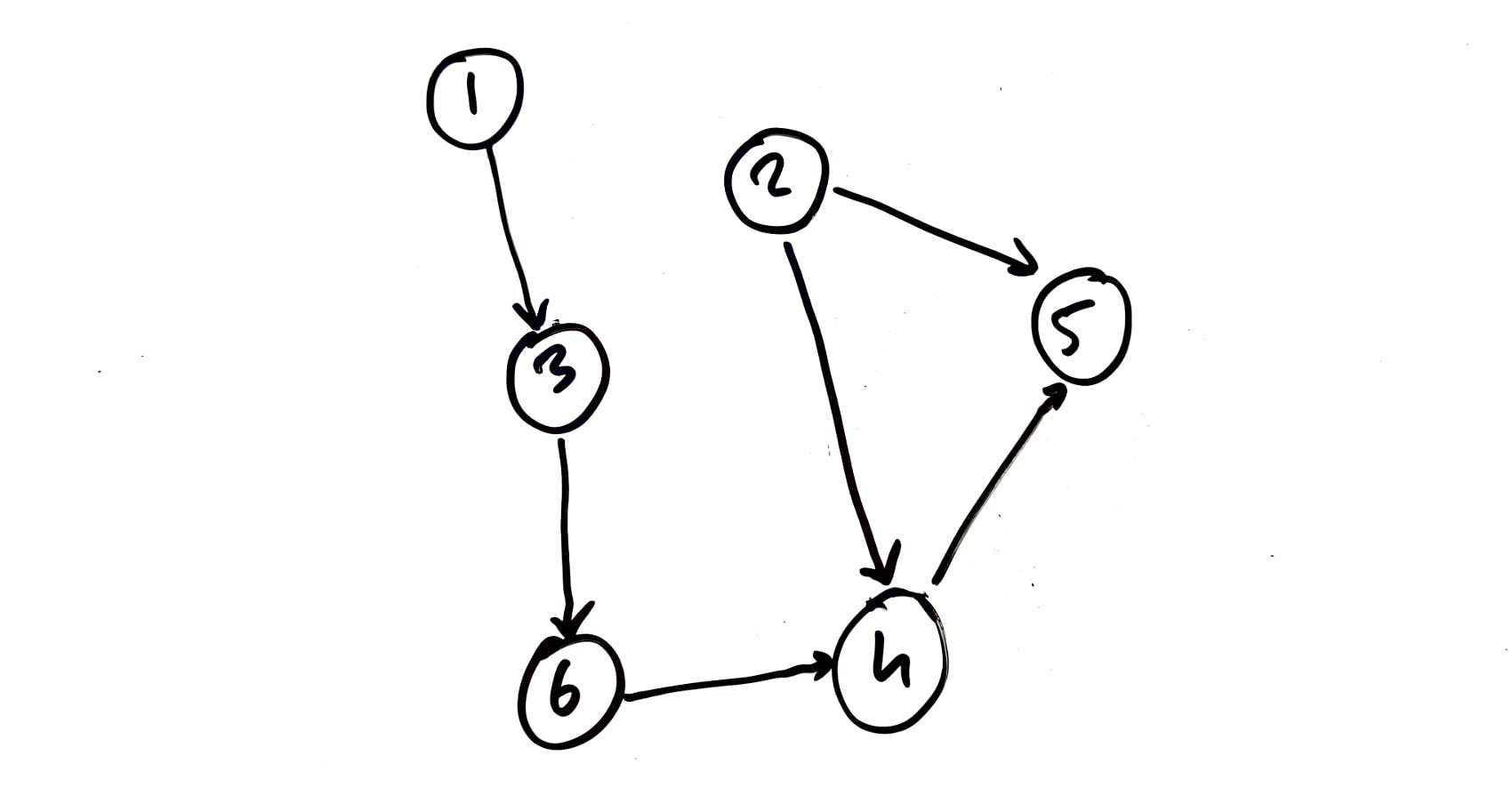
Sparse or Low-Density Network Graph - TechBum.io

2.1. Linked Node Structure or Graph Node

As we saw in the linked list data structure [TODO hyperlink], each Linked List Node connects to another linked list node. Similarly, we can build a Graph Node that can maintain pointers to multiple or any number of other Graph Nodes. Thus, giving us the linked network we often design to visualize a graph on paper.

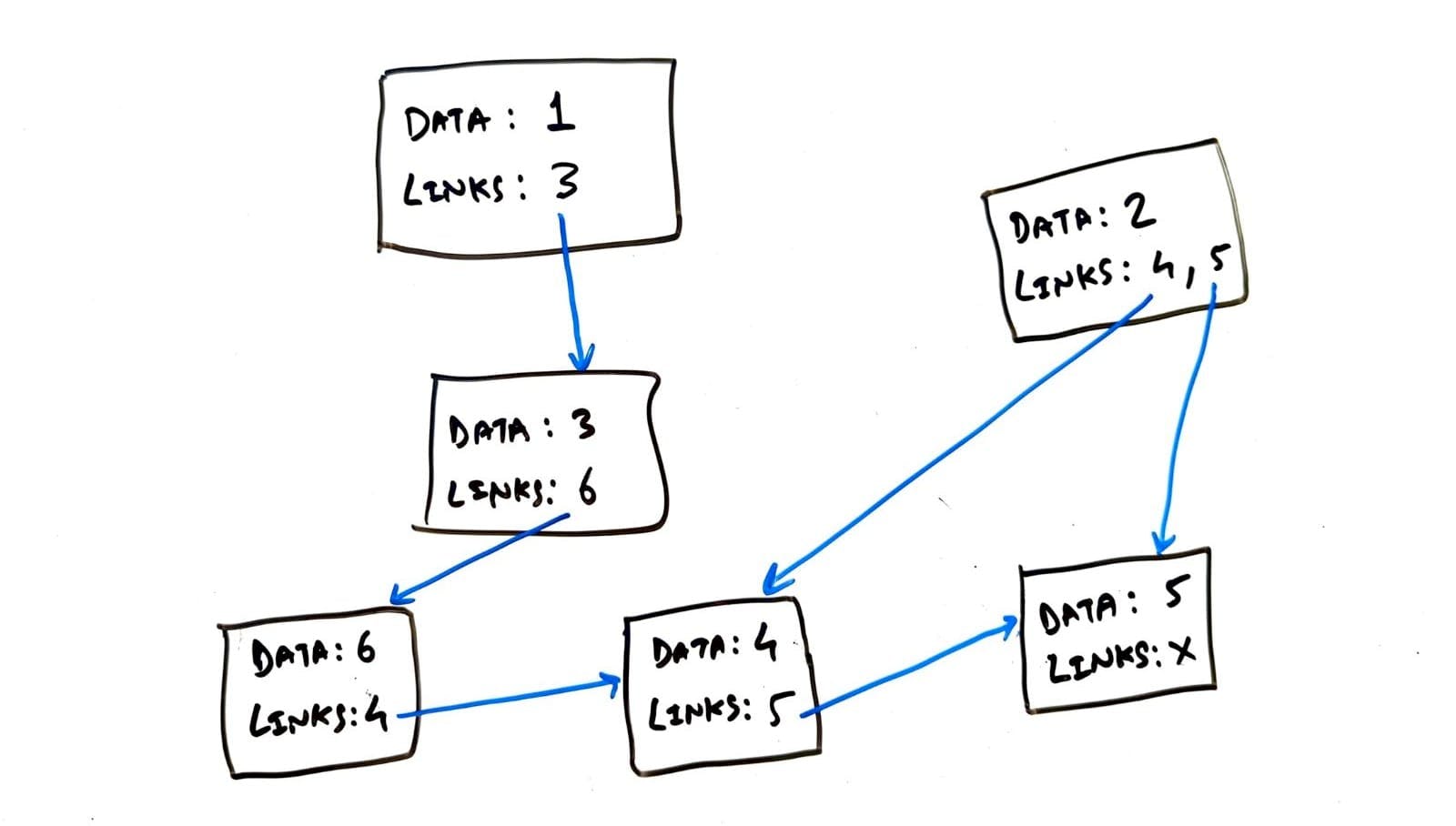
Build a Graph using Graph Nodes - TechBum.io

class GraphNode {
    // any information you want to store for current GraphNode
    Object data;

    // Pointers or Edges to other GraphNodes
    List<GraphNode> links;
}

2.2. Map or Dictionary

A map is yet another way to represent a network and usually works best for coding interview problems. Given that a Map is a set of key-value pairs, to maintain a graph, the key is usually a source node paired with a value that is a list of nodes that the source node connects to.

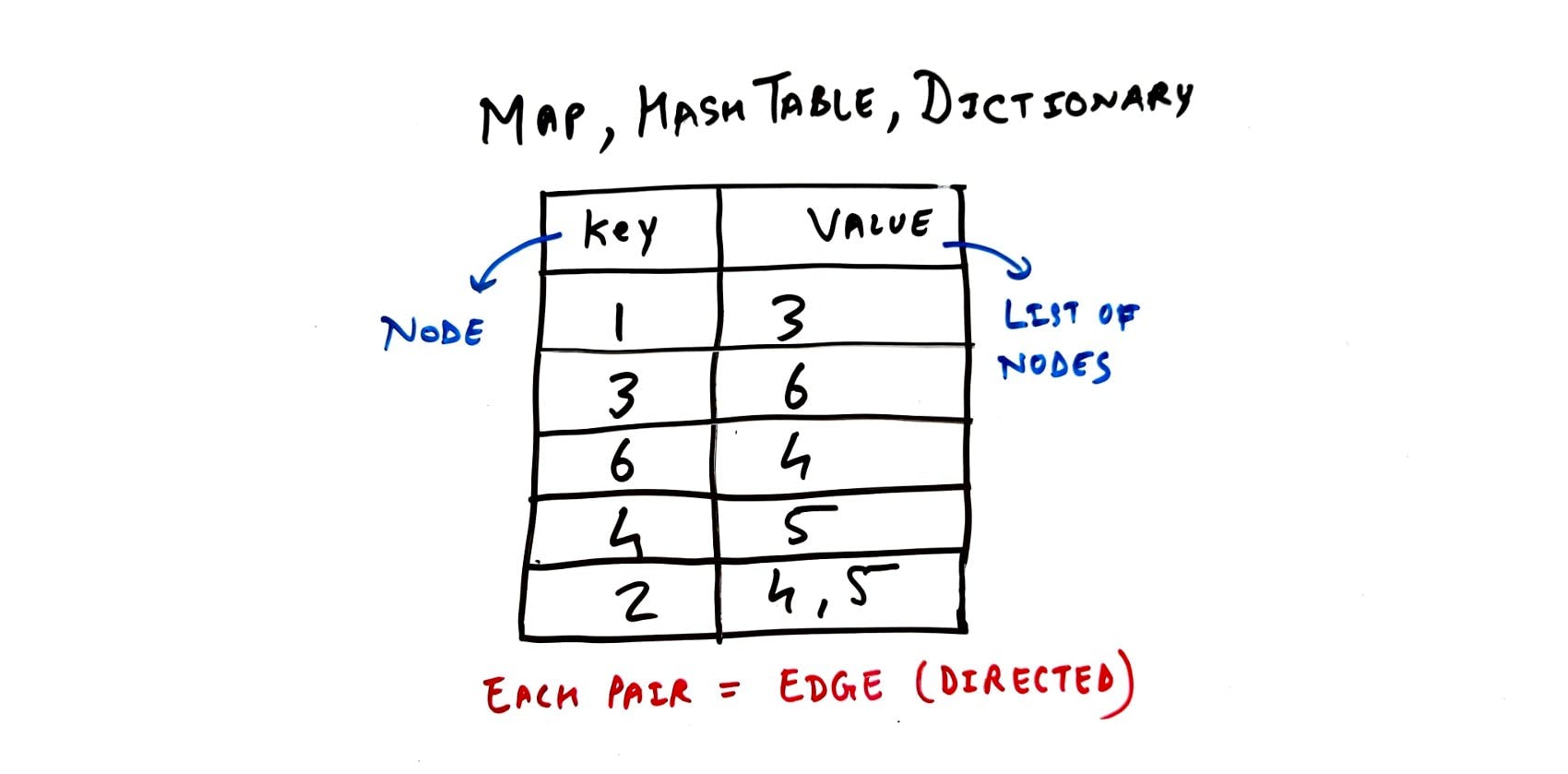
Building Graph using a Map, HashTable or Dictionary - TechBum.io

Directed vs. Undirected Graph

To understand this, think about how connections are made on these two social networks: Facebook and Instagram.

On Facebook, being a "friend" represents an Undirected relationship. If user A sends user B a friend request. A is a friend of B and B is a friend of A, making the relationship bidirectional.

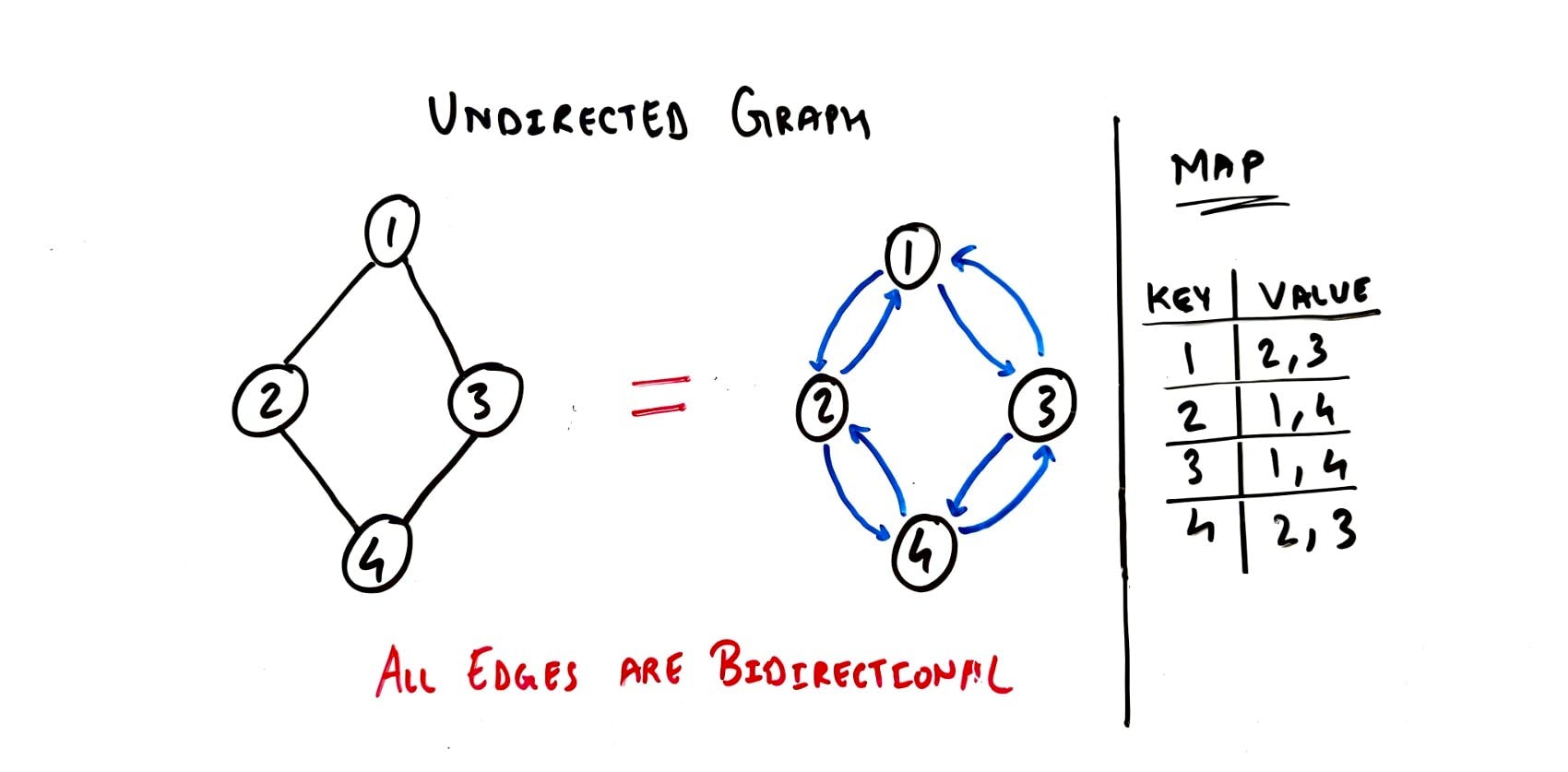
Undirected Graph using Map, HashTable, Dictionary representation - TechBum.io

On Instagram, the followers and following relationship is a Directed relationship. If user A follows B, user B doesn't automatically follow back A. B has to explicitly follow A. This adds the possibility of having a one-way or unidirectional edge.

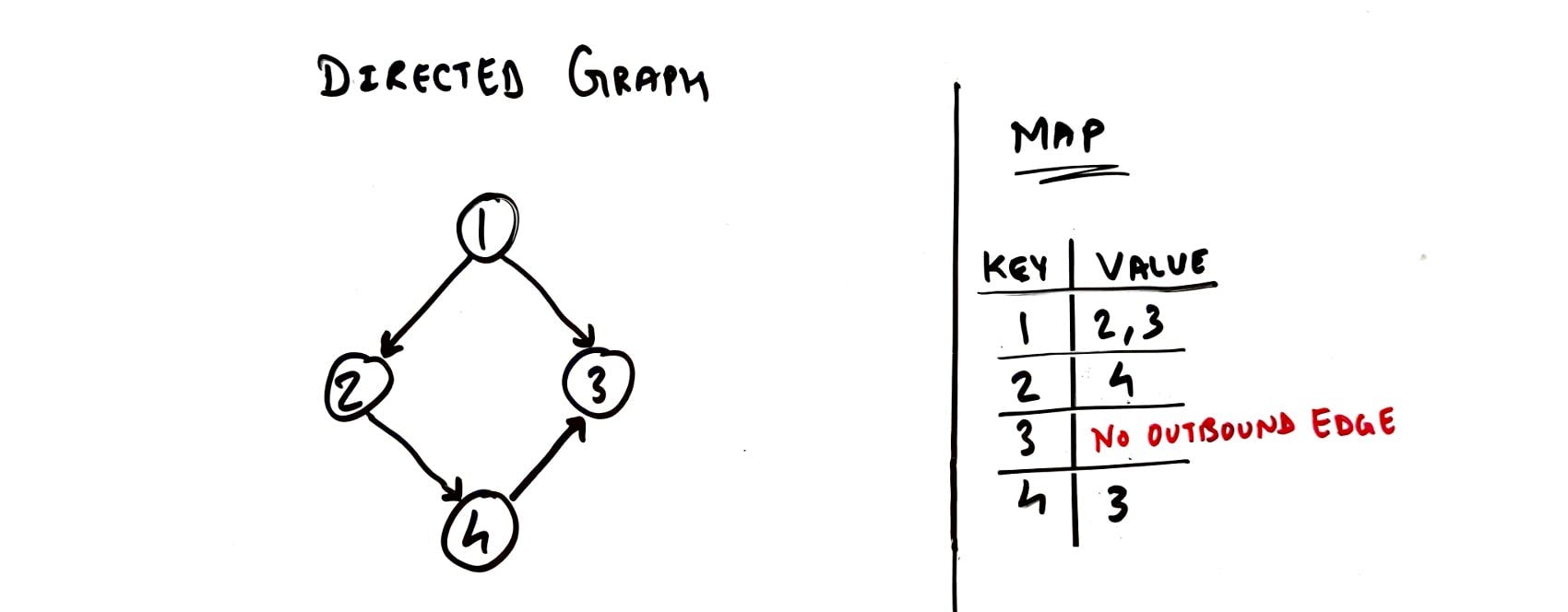
Directed Graph using Map, HashTable, Dictionary representation - TechBum.io

Cyclic vs. Acyclic Graph

Let's take the example of a social network with 3 users: A, B, and C. If A follows B, B follows C and C follows A it creates a loop or a cycle in our network. This is what we call a Cyclic Graph.

💡

All Undirected Graphs are Cyclic, as seen in the above section.

Now take an example of the hierarchy of employment at a company that has a few different employee levels: CEO, Directors, Managers, Programmers. This hierarchy comes from the fact that an employee at each level reports to another employee a level above. Thus forming a Tree-like structure that is usually a unidirectional "reports to" relationship between two nodes. This makes the Tree data structure, which is nothing but a Directed Acyclic Graph.

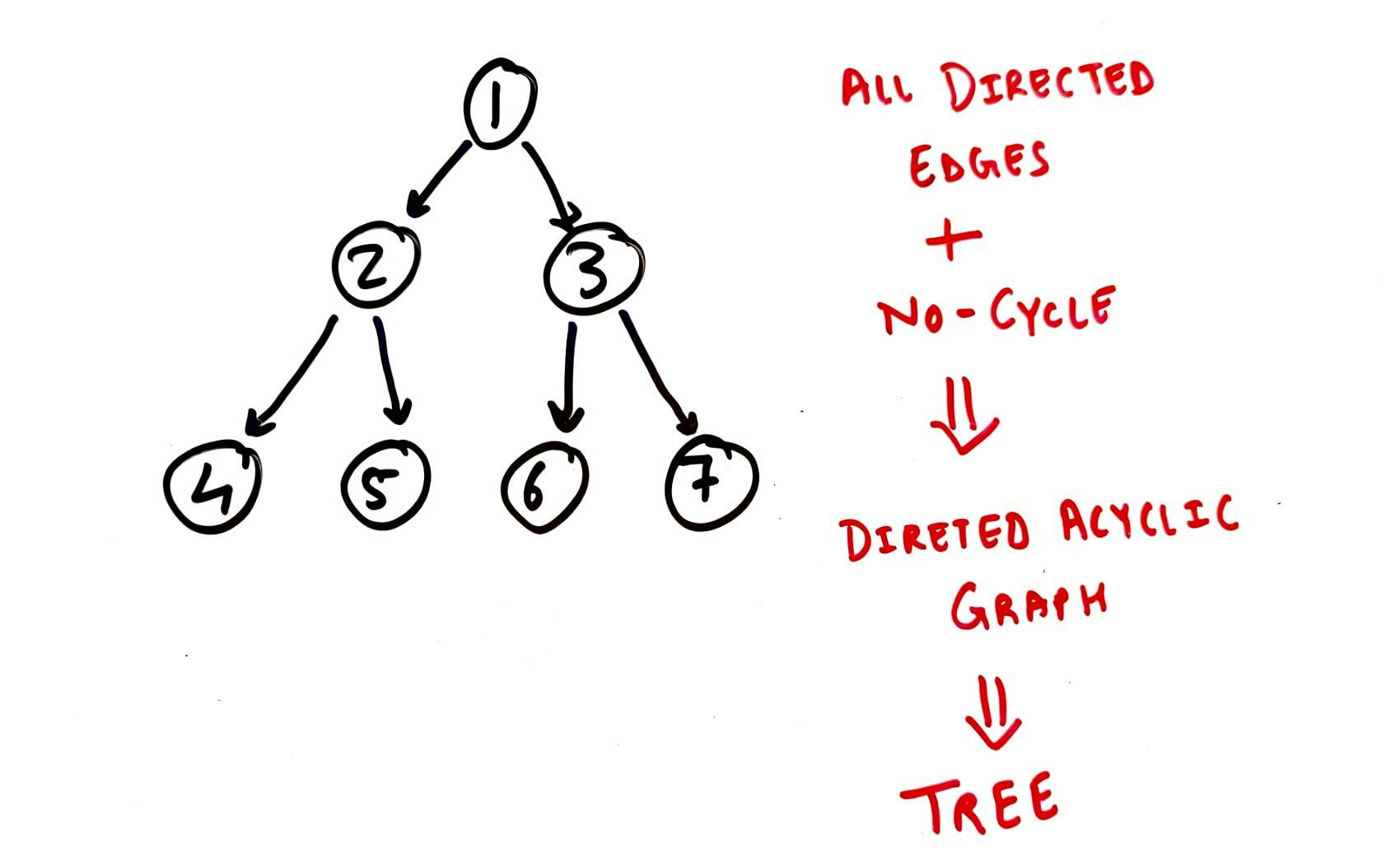
Directed Acyclic Graph or Tree - TechBum.io

To Conclude...

The major takeaway of this tutorial should be the understanding of how to fundamentally translate or represent any graph using either a matrix, map, or linked graph nodes. Equipped with this information, you should now be able to identify, construct and maintain a graph data structure for the most common types of coding interview questions.

Moving on to the following tutorial, we will discuss different traversal techniques like Breadth-First Search and Depth-First Search to move around and navigate our graphs.

---

As always the best form of giving back is to share what you learn. If you found this tutorial helpful or you think it can make a difference for someone else in learning & better preparing for coding interviews, show your support by sharing it with them. Thank you!