Breadth-First Search (BFS) & Depth-first Search are traversal techniques for navigating all types of Graphs. Highly recommend reading the post on graph data structure patterns, which builds a foundation of how Graph representations appear in most coding interview questions. This post aims to teach you a single template for implementing and applying Breadth-first search on any graph coding interview questions.
We will go over the following three parts in this post:
BFS on Network of Nodes
BFS on a Grid or Matrix
BFS template
BFS on a Tree (DAG or Directed Acyclic Graph) or Level Order traversal
Breadth-First Search Algorithm
Bread-First Search(BFS) algorithm is about visiting the immediate neighbors of a Node first before navigating to each neighbor's neighbor in the graph and so on. Let's take the Grid and Network of Nodes graph patterns and see how the BFS algorithm traverses them.
Rule of Thumb: When implementing breadth-first search, you will always use a Queue.
BFS on a Network of Nodes
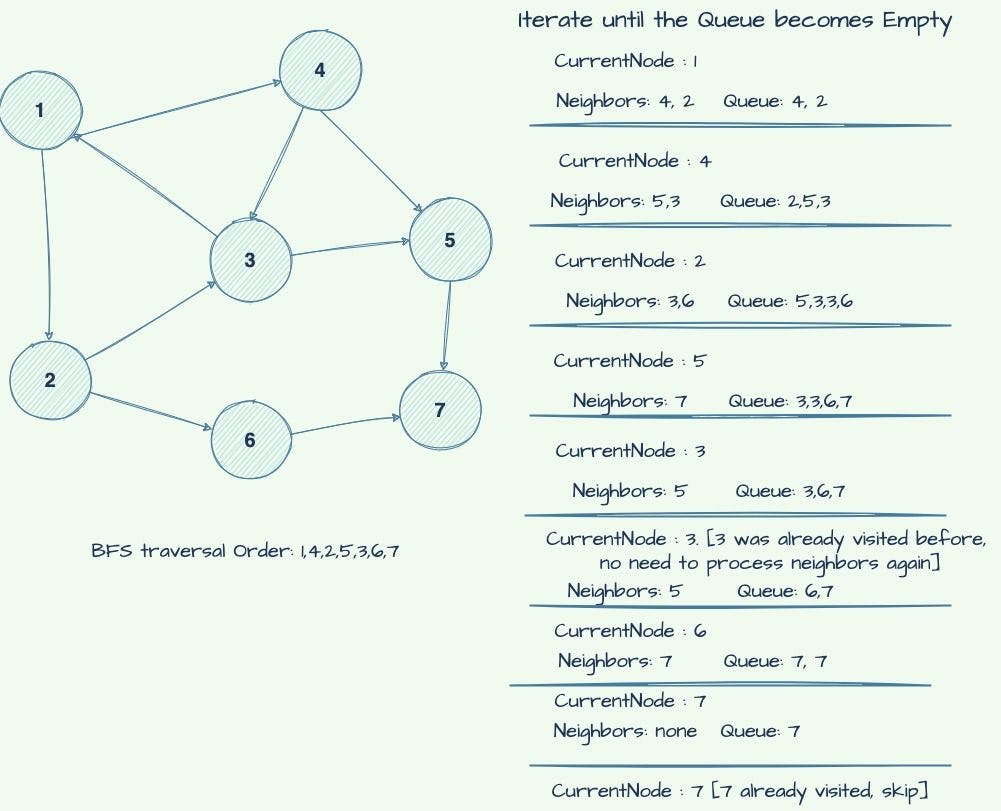
BFS Traversal Also - State of every Iteration
class Node {
Object data;
List<Node> neighbors;
}
public void bfs(Node startNode) {
Queue<Node> q = new LinkedList<>();
Set<Node> visited = new HashSet<>();
q.add(startNode);
while(!q.isEmpty()) {
Node currentNode = q.poll();
if (isVisited(currentNode)) {
continue;
}
doSomethingWithCurrentNode(currentNode);
visited.add(currentNode);
List<Node> neighbors = getNeighbors();
for(Node neighbor: neighbors) {
q.add(neighbor);
}
}
}
public List<Node> getNeighbors(Node currentNode) {
return currentNode.neighbors;
}
public boolean isVisisted(Set<Object> visited, Node currentNode) {
return visited.contains(currentNode);
}
public void doSomethingWithCurrentNode(Node currentNode) {
System.out.println(currentNode.data);
}
BFS on a Grid or Matrix
As we saw earlier in our graph coding interview patterns post, we might be given a graph represented as a grid or table. Let's see how we can apply breadth-first search to a 2-dimensional grid.
public void bfs(Object[][] grid) {
Queue q = new LinkedList<int[]>();
Set visited = new HashSet<int[]>();
int[] startPosition = new int[]{0,0};
q.add(startPosition);
while(!q.isEmpty()) {
int[] currentPosition = q.poll();
if (isVisited(currentPosition)) {
return;
}
int x_corrdinate = currentPosition[0];
int y_coordinate = currentPosition[1];
Object currentNode = grid[currentPosition[x][y];
doSomethingWithCurrentNode(currentNode);
visisted.add(currentNode);
List<int[]> neighbors = getNeighbors(currentPosition);
for (int[] neighbor: neighbors) {
q.add(neighbor);
}
}
}
public List<int[]> getNeighbors(int[] currentPosition) {
List<int[]> neighbors = new Arraylist<>();
neighbors.add(new int[]{x-1,y-1});
neighbors.add(new int[]{x-1,y});
neighbors.add(new int[]{x-1,y+1});
neighbors.add(new int[]{x,y-1});
neighbors.add(new int[]{x,y+1});
neighbors.add(new int[]{x+1,y});
neighbors.add(new int[]{x+1,y+1});
neighbors.add(new int[]{x+1,y-1});
return neighbors;
}
public boolean isVisisted(Set<Object> visited, Node currentNode) {
return visited.contains(currentNode);
}
public void doSomethingWithCurrentNode(Node currentNode) {
System.out.println(currentNode.data);
}
Now that we see two examples of applying BFS to different graph representations, observe the similarity in the steps above. We can build out a generic template for this coding interview pattern.
BFS Algorithm Template
public void bfs(Node startNode) {
Queue q = new LinkedList<Object>();
Set visited = new HashSet<Object>();
q.add(startNode);
while(!q.isEmpty()) {
Node currentNode = q.poll();
if (isVisited(currentNode)) {
continue;
}
doSomething(currentNode);
List<Node> neighbors = getNeighbors();
for(Node neighbor: neighbors) {
q.add(neighbor);
}
doSomething(currentNode);
}
}
public List<Node> getNeighbors(Node currentNode) {
}
public boolean isVisisted(Set<Object> visited, Node currentNode) {
return visited.contains(currentNode);
}
public void doSomething(Node currentNode) {
}
Level Order Traversal or BFS on a Tree (DAG)
The Tree data structure is just another type of Graph, precisely, a Directed Acyclic Graph (DAG). Breadth-first search can be applied to a DAG or Tree using the same template above. BFS traversal on a tree is also referred to as a Level-Order traversal.
public class TreeNode {
Object data;
List<TreeNode> children;
}
public void bfsOnTree(TreeNode startNode) {
Queue<TreeNode> q = new LinkedList<>();
q.add(startNode);
while(!q.isEmpty()) {
TreeNode currentNode = q.poll();
doSomething(currentNode);
List<TreeNode> neighbors = getNeighbors(currentNode);
for (TreeNode neighbor: neighbors) {
q.add(neighbor);
}
}
}
public List<TreeNode> getNeighbors(TreeNode currentNode) {
return currentNode.children;
}
public void doSomething(TreeNode currentNode) {
System.out.println(currentNode.data);
}
I recommend opening two browser tabs side-by-side and comparing the level order traversal on a tree with the generic graph BFS template. You will notice we have skipped parts related to maintaining a visited set of nodes. We don't need to maintain a visited set because Tree is a Directed-Acyclic graph. When we retrieve the current Node (call it A) and then process one of its neighbors(call it B). When we try to find neighbors of B, we will not see A as Node B doesn't point to Node A. This optimizes our space complexity when applying breadth-first search on a tree data structure.
In the next post, we will learn the Depth-First search traversal pattern and create a generic template as we did for the above BFS pattern that can be applied to any graph.
